最大子数组和问题

1.背景

问题：给定n个整数（可能为负数）组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0，依此定义，所求的最优值为： Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n。

例如，当（a[1],a[2],a[3],a[4],a[5],a[6]）=(-2,11,-4,13,-5,-2)时，最大子段和为20。

-- 引用自

2.分析

  要求序列子段和的最大值，假设最优值为： Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n；在这里我们设置 \(sum_{n}\) 为n个数的和，max为最大和，分析以下情况：

1.如果和最大，那么这个序列首位必然为正数，第一个正数之前的序列去掉，此时(\(sum_{n}\) =\(sum_{n-1}\) +a[n])<a[n] ；

2.如果一段序列和 \(sum_{n}\) 由正数逐渐变为负数或0，则这段序列去掉，此时( \(sum_{n}\) = \(sum_{n-1}\) +a[n])<a[n]， 重新计算之后的序列和 \(sum_{n+1}\)；

3.如果整个序列和为负数，则取max=0;

  如果没有以上情况，每计算一次序列和就将计算所得值与上一次计算所得值比较，如果\(sum_{n}\) > max;则 max = \(sum_{n}\);如此递归，最终求得最大子段和。

递推求最大值公式如下：

max=MAX(\(sum_{n}\)=\(sum_{n-1}\)+a[n],max)；\(sum_{0}\)=0;

3.代码及测试

• 代码地址

• 源代码

//源程序代码#include
    
     #include
     
      using namespace std;int maxarray(int*a,int le){    int len = le;    int sum = 0, max = 0, i;//  int *b = new int[len];//  b[0] = a[0];    for (i = 0; i < len; i++)    {        sum = a[i] + sum;        if (sum < a[i])            sum = a[i];        if (sum > max)            max=sum;    /*  if (b[i - 1] > 0)        {            if (i == 1) max = b[0];            b[i] = b[i - 1] + a[i];        }        else            b[i] = a[i];        if (b[i] > max)            max = b[i];  */    }    return max;}int main(){    int len, i;    cin >> len;    if (len <= 0) return 0;    int *array = new int[len];    for (i = 0; i < len; i++)    {        cin >> array[i];    }    cout << maxarray(array,len) << endl;    delete [] array;    system("pause");    return 0;}
     
    

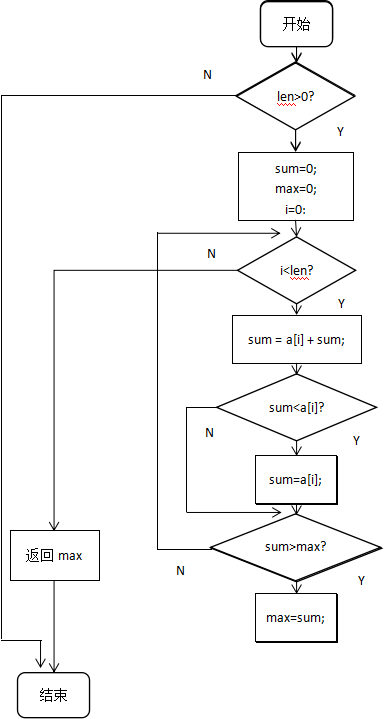
• 流程图

  

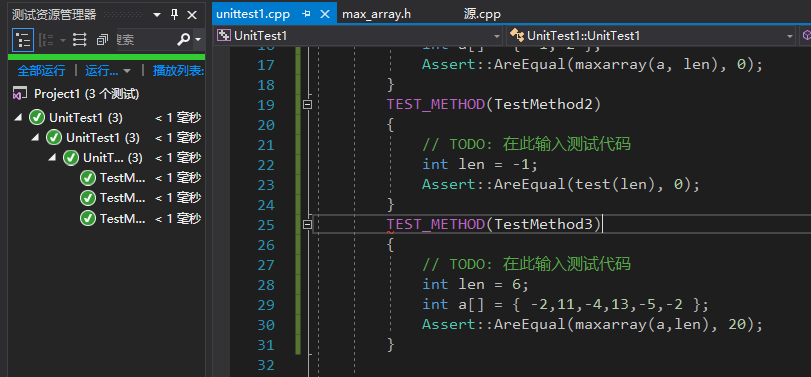
• 单元测试

  本次测试采用条件测试，分为三种情况:
  • 数组值全为负数，此时应返回0，测试数组a[] = { -1,-2 };
  • 数组长度小于等于0，此时返回0，测试长度 len=-1;
  • 包含sum<a[i],sum>a[i],sum<max,sum>max条件，并返回最大值，测试数组a[] = { -2,11,-4,13,-5,-2 }；

• 测试代码

//测试代码                TEST_METHOD(TestMethod1)        {            // TODO: 在此输入测试代码            int len = 2;            int a[] = { -1,-2 };            Assert::AreEqual(maxarray(a, len), 0);        }        TEST_METHOD(TestMethod2)        {            // TODO: 在此输入测试代码            int len = -1;            Assert::AreEqual(test(len), 0);        }        TEST_METHOD(TestMethod3)        {            // TODO: 在此输入测试代码            int len = 6;            int a[] = { -2,11,-4,13,-5,-2 };            Assert::AreEqual(maxarray(a,len), 20);        }

• 测试结果